Bienvenido a las matemáticas de los años veinte

Gracias a una reciente publicación en Twitter de Brette Garner en la Universidad de Denver, me encontré con un interesante artículo del NCTM (Consejo Nacional de Maestros de Matemáticas) publicado en The Mathematics Teacher. El título de la revista es “Efecto de ciertos tipos de ejercicios de velocidad en aritmética” por A.I. Messick El estudio dividió a 272 alumnos de cuarto y quinto grado en dos grupos mientras enseñaba la adición: uno centrado en la velocidad y el otro centrado en la precisión. Estas son algunas de las conclusiones: (1) La precisión es más importante que la velocidad, (2) Desde el punto de vista de la velocidad, hace poca diferencia lo que se enfatiza, velocidad o precisión, (3) Desde el punto de vista de la precisión, es es mucho mejor enfatizar la precisión, y (4) Además de enseñar a los alumnos de cuarto y quinto grado de las escuelas primarias, es mejor enfatizar la precisión en lugar de la velocidad.
Dado el trabajo reciente de la profesora Jo Boaler y su grupo en Stanford y la definición de fluidez matemática del NCTM como precisa, flexible y eficiente con los cálculos, la investigación concluye que la precisión de la enseñanza sobre la velocidad no es una sorpresa. Lo que encontré sorprendente; sin embargo, es que este artículo fue publicado en 1926. No en 1996, ni en 2006 ni en 2016, sino en 1926. Desde 1926, ¿cuántos miles de estudiantes han sufrido a través de las matemáticas cronometradas, a menudo conocidas como “minutos locos” que se centran en la velocidad? ¿Cuántos estudiantes se desanimaron de estudiar ingeniería, ciencias, medicina u otras disciplinas porque pensaban que ser bueno en matemáticas significaba memorizar procedimientos y regurgitar datos rápidamente? ¿Cuántos científicos no pudimos crear desde 1926 porque memorizar procedimientos matemáticos fue un guardián para seguir estudiando todas las ciencias?

Pero, espera. 8 x 7 es siempre 56, ¿verdad? Solo tienes que saber eso rápidamente. Si no puede recordar esto de inmediato, entonces, ¿cómo puede estudiar fracciones o resolver ecuaciones diferenciales? Yo diría que saber cómo calcular 8 x 7 de manera flexible, precisa y eficiente es mucho más significativo que el recuerdo rápido o la memorización.
Cuando era maestra de secundaria, encontré demasiados estudiantes que no podían responder preguntas como “¿Cuánto es 8 x 7?” Cuando a los estudiantes se les enseña su tabla de tiempos a través de “minutos locos” u otras técnicas que dependen de la velocidad, pueden recordarlos a corto plazo, pero no podrán recordarlos años más tarde. En particular, muchos estudiantes de secundaria lucharon por recordar la tabla del 8. A veces cuando les preguntaba la respuesta a 8 x 7, soltaban 52, 58 u otra respuesta incorrecta. Cuando dije “no”, por lo general me miraban con una mirada perpleja, se encogían de hombros y decían: “Hmmmm … no sé”, o buscaban su calculadora.
En lugar de renunciar o confiar en la tecnología para hechos simples, quiero vivir en una sociedad de personas que, cuando olvidan un hecho simple como 8 x 7, tienen otra forma de resolverlo de manera eficiente. Un escenario posible: no puedo recordar 8 x 7, pero sé que 10 x 7 es 70 y necesito quitar 2 x 7, que es 14, dejándome con 56. Entonces, 8 x 7 es 56. Hay muchas otras formas de responder a esta pregunta sin usar lápiz y papel ni depender de una calculadora, esto es matemática mental verdadera porque se basa en la resolución de problemas y hacer conexiones entre varios números y operaciones. Lamentablemente, muchas personas equiparan las matemáticas mentales con los “minutos locos” y la rápida regurgitación de los hechos. Un estudiante que comprende múltiples formas de calcular 8 x 7 exhibe un verdadero sentido numérico, si confiamos únicamente en los procedimientos de memorización y memorización, producimos estudiantes y adultos que solo tienen una forma de abordar una pregunta como 8 x 7. Cuando su memoria falla, no saben qué hacer para encontrar la respuesta.
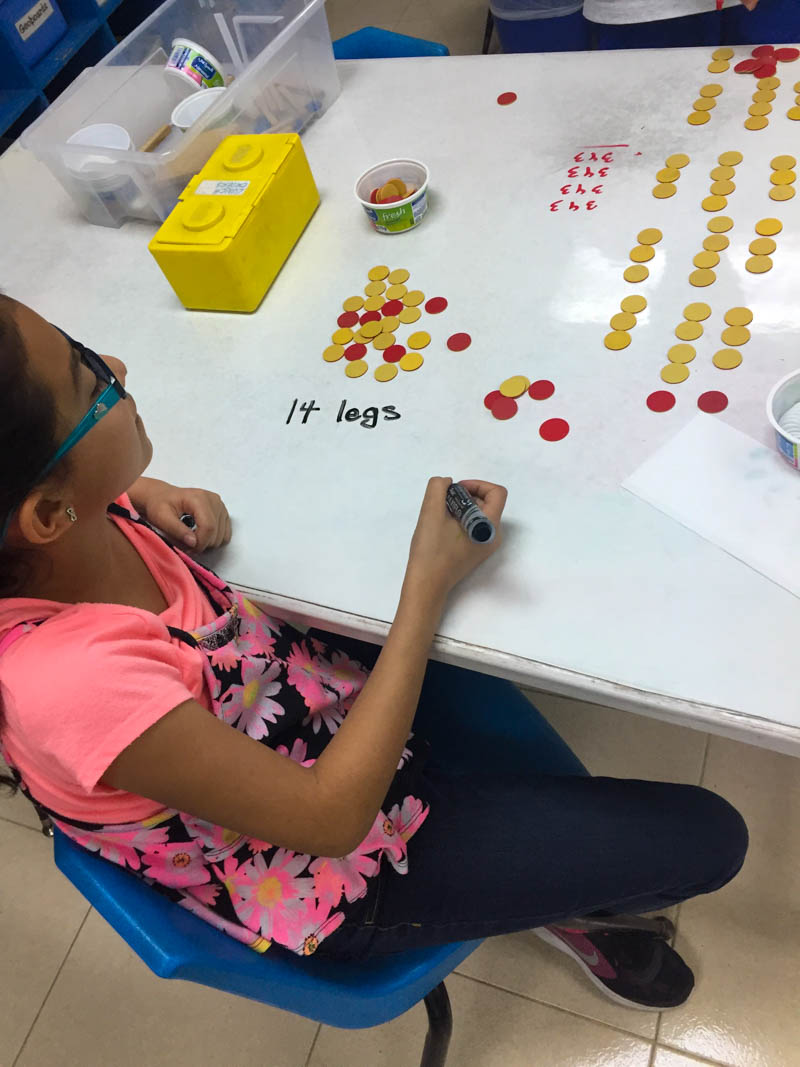
Making Math Moments that Matter, un podcast y un maravilloso sitio web curado por Kyle Pearce & John Orr, tuiteó recientemente que “enseñar matemáticas exclusivamente desde su libro de texto es como enseñar con una bolsa sobre su cabeza”. Esa declaración realmente resuena conmigo porque cuando los maestros enseñan únicamente a partir de un texto, están enseñando una visión muy unidimensional de las matemáticas. ¿Con qué otro tipo de actividades podrían participar los estudiantes para aprender el contenido? ¿Qué preguntas podrían venir solos si se les dan menos indicaciones y procedimientos para imitar? ¿Qué tecnología existe actualmente que podría no haber estado disponible cuando se publicó el libro de texto? Dado lo que sabemos sobre las mejores prácticas actuales en matemáticas, ¿cómo pueden los maestros quitarse las bolsas de papel de la cabeza?
Para explorar estas ideas, reflexiono sobre mi viaje como maestra de matemáticas de secundaria. Cuando comencé a enseñar, seguía mucho el libro de texto y tenía esa bolsa de papel firmemente plantada sobre mi cabeza. De hecho, recuerdo las primeras semanas en mi primera escuela internacional en Caracas en 1999. El pedido de libros se retrasó y no se entregó. ¿Cómo podría enseñar matemáticas IB sin un libro de texto? El simple pensamiento me paralizó, pensé que era una buena maestra porque era buena para explicar los procedimientos que se encuentran en los libros de texto a mis alumnos, si dejaba mis explicaciones claras en su entrega, estaba haciendo mi trabajo. Había perdido todo el punto al centrarme en lo que estaba haciendo en lugar de en lo que los estudiantes están aprendiendo. Como consultora en matemáticas, ahora apoyo a los maestros hoy en día para descubrir cómo se pueden aprender las matemáticas a través de las aplicaciones y la resolución de problemas. Como nueva maestro, solo ofrecí servicios para resolver problemas, mis primeros alumnos resolvieron los problemas verbales que se encuentran al final del capítulo y resolvieron muy poco los problemas verdaderos.
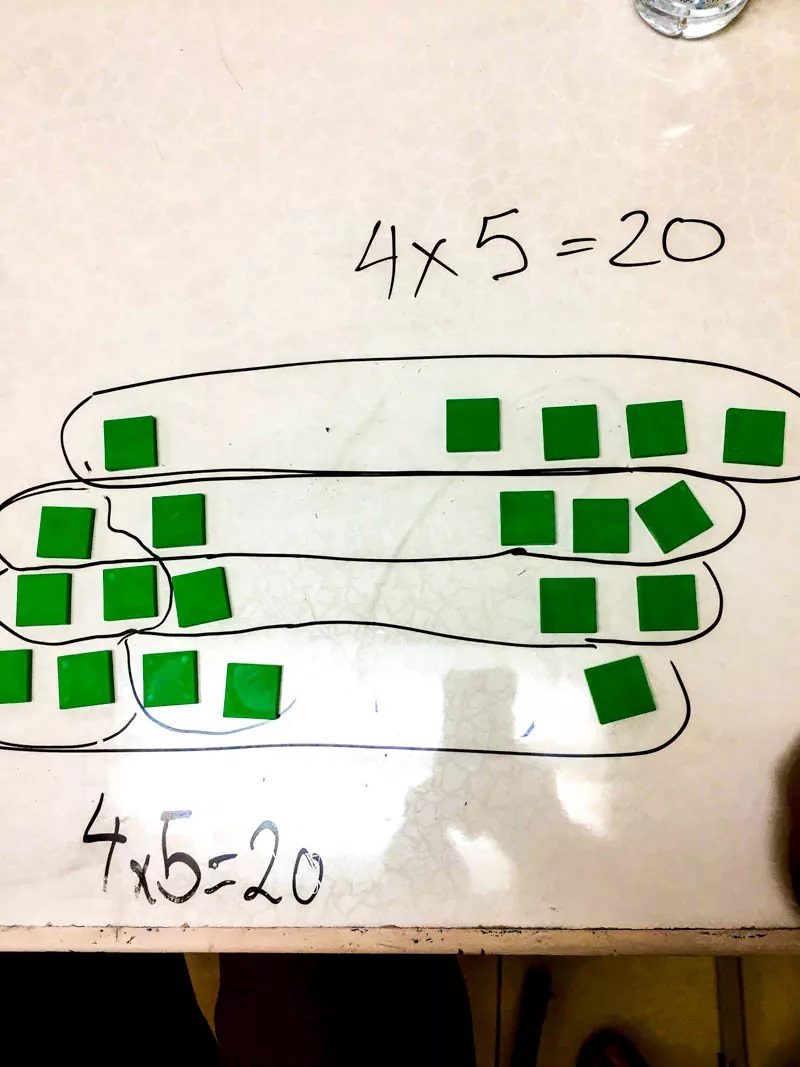
¿Qué cambió en mi pensamiento y en mi práctica? ¿Cómo quité la bolsa de papel de mi cabeza? Tuve que aprender a dejar ir comenzando con algo pequeño y confiando en que mis alumnos aún aprenderían el contenido necesario. Esto no fue fácil para mí y puede dar mucho miedo, me encantó ser el sabio en el escenario, me sentí cómodo allí y recibí comentarios positivos de los estudiantes que me dijeron que disfrutaban mis clases de matemáticas. Mirando hacia atrás en mis primeros días como profesora, no estaba enseñando muchas matemáticas, estaba enseñando trucos, procedimientos y “cómo hacerlo”. Era un experto en ayudar a los estudiantes a entender los problemas de los libros de texto, lo que significaba explicarles claramente los procedimientos y trucos. Lo que no estaba haciendo era crear experiencias para que mis alumnos fueran verdaderos solucionadores de problemas.
¿Cómo podemos proporcionar a todos los estudiantes la oportunidad de resolver problemas y dar sentido a las matemáticas que están aprendiendo? ¿Cómo pueden los maestros cambiar su instrucción de matemáticas? Ofrezco tres sugerencias:
- Empieza pequeño.
- Encuentre una red de aprendizaje profesional (PLN).
- Incluya estudiantes y padres en la conversación.
Comenzar con algo pequeño es a menudo una de las cosas más difíciles para los educadores. Si hay una mejor manera de hacer las cosas, entonces tengo que tirar el libro de texto mañana, encontrar todos mis recursos basados en los estándares y pasar cinco horas preparándome para cada lección. No. En cambio, tome una cosa de una lección y cámbiela, considere un resultado de aprendizaje de una lección y encuentre un problema interesante (muchos lugares para comenzar aquí) que implique más pensamiento de los estudiantes y menos dirección del maestro. Si nunca ha hecho esto antes, puede ser muy difícil dejarlo ir. Nota: no tiene que resolver sus propios problemas al principio, puede probar un problema abierto o youcubed. Aquí hay un ejemplo de Jo Boaler:

Ambas preguntas exploran el concepto de área, pero el segundo permite la exploración de los estudiantes, la creatividad y las conversaciones sobre qué área significa.
En segundo lugar, únase a un PLN con otros educadores que también estén interesados en enseñar matemáticas de manera diferente. Pueden estar en tu escuela o en todo el mundo. Puede ser a través de un grupo de amigos críticos o a través del trabajo con un entrenador de instrucción, no hay nada mejor que poder compartir un éxito, por pequeño que sea, con colegas de apoyo. Twitter es un excelente lugar para comenzar, aprendo mucho en Twitter de las personas de matemáticas y educación a quienes sigo. Existe una gran cantidad de información y puede ser selectivo sobre lo que aparece en su feed. Puede encontrar un compañero maestro que viva en un país diferente, pero con quien se conecte y comparta ideas geniales, hay grupos de Facebook dedicados a la enseñanza de las matemáticas. No tenga miedo de exponerse virtualmente o en persona.

Finalmente, informe a sus alumnos sobre lo que está haciendo. Si se les ha enseñado tradicionalmente durante años, están acostumbrados a sentarse y obtener la información del sabio en el escenario. Este tipo de aprendizaje pasivo es mucho más fácil que tener que involucrarse en la resolución de problemas, si no entienden por qué estás haciendo las cosas de manera diferente y los prepara para ello, puede haber un retroceso innecesario. Algunas veces, cuando se utiliza un enfoque de “estudiante como trabajador, maestro como entrenador” para la instrucción, los estudiantes asumen que no conoce las respuestas. Si al principio les dice que realmente conoce las respuestas, creo que están más dispuestos a investigar los problemas. Solía decirles a mis alumnos: “Sí, sé las respuestas a las preguntas en las que están trabajando. No, no te lo voy a decir aunque lo sepa”. También compartí esta información durante la noche de los padres. Tuve muy poco rechazo de los padres porque los invité a la conversación y les di los recursos para apoyar a sus hijos fuera del aula, si la clase de matemáticas de su hijo se ve diferente, nuestro trabajo como educadores es ayudar a los padres a navegar esto de lo contrario, puede conducir a información errónea viral, como el padre que escribió un cheque usando matemática Common Core.
Mi viaje de profesora de procedimientos, profesora de matemáticas y consultora de matemáticas no ha sido lineal. De hecho, ha sido todo menos eso. Continuamente estoy creciendo y aprendiendo a medida que continúo en este camino, me gusta apoyar a los maestros a medida que encuentran sus propios caminos para enseñar más sobre la belleza de las matemáticas y menos procedimientos, me convertí en consultora en matemáticas porque me apasiona capacitar a los educadores con la experiencia matemática necesaria para inspirar a los solucionadores de problemas del futuro, me encanta compartir mis triunfos y fracasos de una manera vulnerable para ayudar a los maestros principiantes y experimentados a crecer. ¿Hay algo que le gustaría hacer de manera diferente en su clase de matemáticas? Pruébelo hoy. Dé el primer paso y hágame saber cómo va.
Este artículo está disponible y se puede acceder a él en inglés aquí.
Recursos adicionales / Lectura:
Boaler, J., & Dweck, C. S. (2016). Mathematical Mindsets: Unleashing Students’ Potential Through Creative Math, Inspiring Messages and Innovative Teaching. First edition. San Francisco, CA: Jossey-Bass; a Wiley Brand.
Brettegarner. (2020, Jan 5). This 1926 study found that emphasizing speed in basic fact drills is not good for students. Practice with an emphasis on accuracy, however, improved speed and accuracy. [Tweet]. Retrieved from https://twitter.com/brettegarner/status/1213605204311982082
Fedio, N. (2019). Information Overload. Retrieved from https://www.mathematique.us/blog/information-overload
Gojak, L. (2012) Fluency: Simply Fast and Accurate? I Think t! Retrieved from https://www.nctm.org/News-and-Calendar/Messages-from-the-President/Archi ve/Linda-M_-Gojak/Fluency_-Simply-Fast-and-Accurate_-I-Think-Not!/
MakeMathMoments. (2019, Dec 29). Teaching math exclusively from your textbook is like teaching with a bag over your head. [Tweet]. Retrieved from https://twitter.com/MakeMathMoments/status/1211383831368028164
Messick, A.I. (1926). EFFECT OF CERTAIN TYPES OF SPEED DRILLS IN ARITHMETIC. The Mathematics Teacher Vol. 19, No. 2. 104-109. Retrieved from https://www.jstor.org/stable/27950803?seq=1
Open Middle. (2020). Retrieved from https://www.openmiddle.com/
Pelletiere, N. (2015). Dad Writes Gag Check to Son’s Elementary School Using Common Core Math. Retrieved from https://abcnews.go.com/Lifestyle/dad-writes-gag-check-sons-elementary-school-common/story?id=33932439
Reuell, P. (2019) Study shows students in ‘active learning’ classrooms learn more than they think. Retrieved from https://news.harvard.edu/gazette/story/2019/09/study-shows-that-students-learn-more-when-taking-part-in-classrooms-that-employ-active-learning-strategies/