José María Arias Cabezas | @AriasCabezas

November 2, 2023

• Enseñar y Aprender

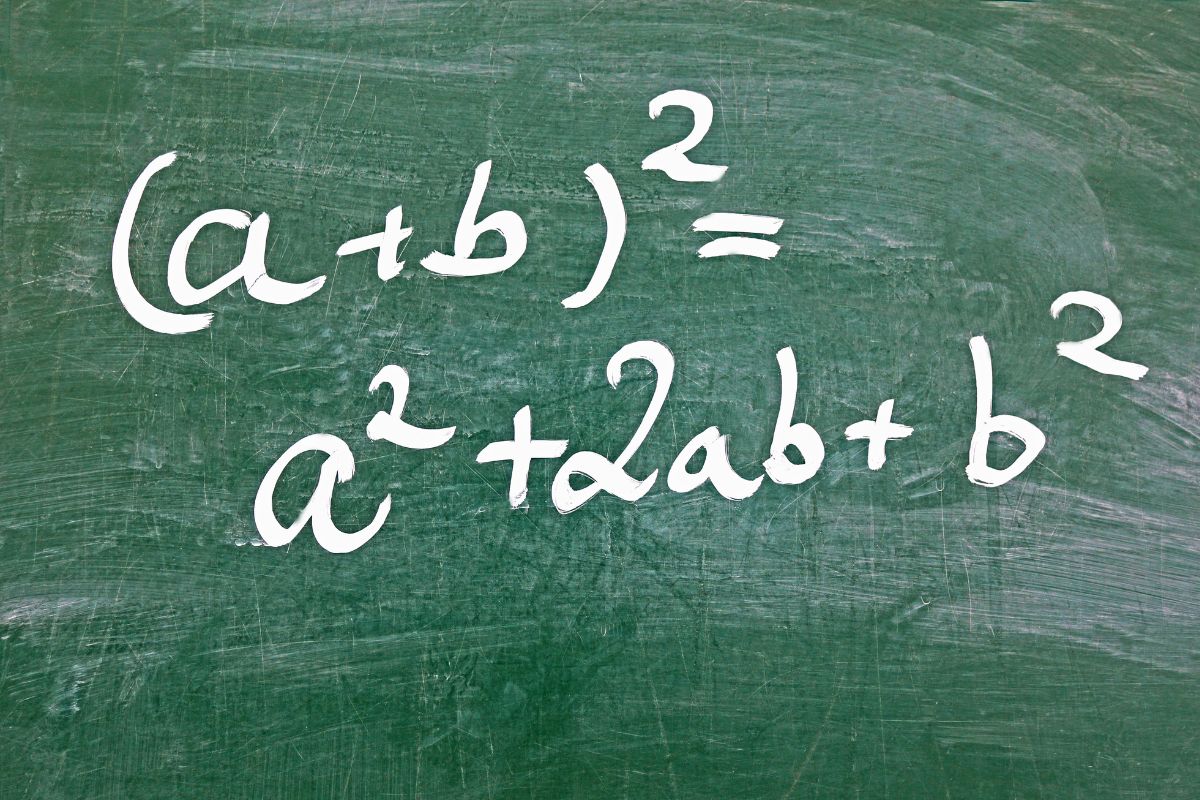
Vamos a practicar la resolución de problemas algebraicos mediante la descomposición en partes, la automatización y el pensamiento algorítmico utilizando applets de GeoGebra.

PROCEDIMIENTO DE RESOLUCIÓN DE PROBLEMAS MEDIANTE ECUACIONES

Sesión 1

EXPLICA

Halla las longitudes de los lados de un triángulo rectángulo sabiendo que son tres números enteros pares consecutivos.

Abre el applet: Procedimiento de resolución de problemas mediante una ecuación

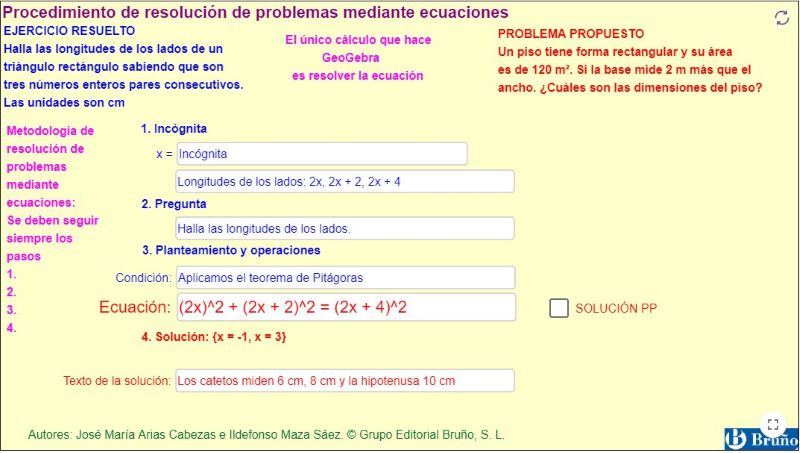
Analiza la resolución del PROBLEMA RESUELTO mediante la descomposición de las siguientes partes:

1. Incógnita: se escribe el concepto de la incógnita.
2. Pregunta: se escribe la pregunta o preguntas.
3. Planteamiento y operaciones: se escribe la relación o condición que se convierte en ecuación y se resuelve
4. Solución: se escriben la solución con las unidades y se comprueba que son coherentes y que se cumplen las relaciones dadas.

ELABORA

Resuelve el PROBLEMA PROPUESTO y comprueba la solución.

Sesión Final

Una vez realizados los problemas anteriores, y que ya tienes soltura suficiente como para no tener que escribir todos los pasos del planteamiento. Ha llegado el momento de utilizar solo el programa o herramienta con el menor número de pasos posibles para resolver problemas. Así utilizarás la esencia de las matemáticas, es decir, que te dediques solo a pensar y que todas las operaciones las resuelva el programa.

ELABORA

1. Entre Sonia y Alba tienen 300 €. Alba tiene el triple de dinero que Sonia. ¿Cuánto dinero tiene cada una?
2. La población de una cierta especie animal en peligro de extinción se reduce según la fórmula P = 5000 · 2^–0,3x, donde P es la población final, y x, el número de años. Si se considera que la extinción es inevitable si hay menos de 100 ejemplares. ¿En cuántos años se alcanzará el punto en el que se considera que la extinción es inevitable?

Cuando ya tengas soltura en la resolución de problemas de ecuaciones no es necesario que realices todos los pasos, con escribir la ecuación es suficiente. De esta forma puedes seguir resolviendo todos los problemas que se resuelvan mediante una ecuación.

2. PROCEDIMIENTO DE RESOLUCIÓN DE PROBLEMAS MEDIANTE SISTEMAS 2×2

Sesión 1

EXPLICA

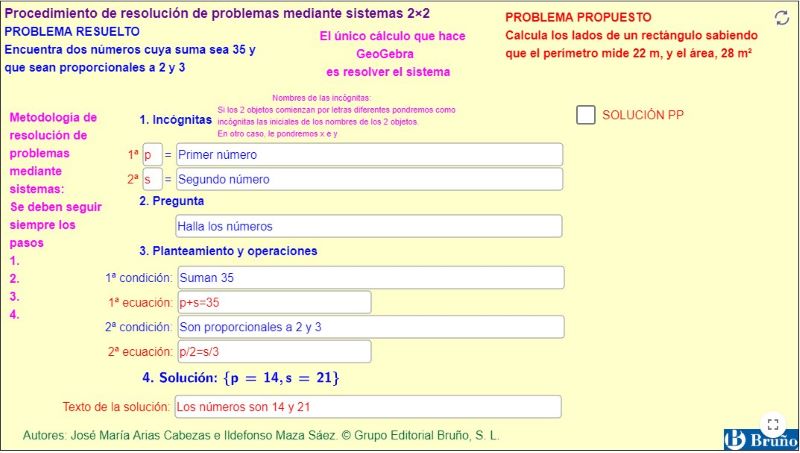
Encuentra dos números cuya suma sea 35 y que sean proporcionales a 2 y 3

Abre el applet: Procedimiento de resolución de problemas mediante sistemas 2×2

https://www.geogebra.org/m/pyrdrrrv

Analiza la resolución del PROBLEMA RESUELTO mediante la descomposición de las siguientes partes:

1. Incógnitas: se escriben los conceptos de las incógnitas.
2. Metodología y didáctica: Si los objetos comienzan por letras diferentes, pondremos como incógnitas las iniciales de sus nombres. En otros casos pondremos x e y, si conocemos qué valor es el menor y el mayor, debemos asociar el valor de la 1.ª incógnita x al valor más pequeño y el de y al mayor. Estas recomendaciones ayudan a los alumnos a centrarse en el problema y adquieren mucha más soltura en la resolución de problemas algebraicos.
3. Pregunta: se escribe la pregunta o preguntas.
4. Planteamiento y operaciones: se escriben las relaciones o condiciones que se convierten en ecuaciones formando un sistema y se resuelve.
5. Solución: se escriben la solución con las unidades y se comprueba que son coherentes y que se cumplen las relaciones dadas.

ELABORA

Resuelve el PROBLEMA PROPUESTO y comprueba la solución.

Sesión Final

Al igual que en los problemas de ecuaciones, resuelve los siguientes problemas escribiendo solo las ecuaciones.

ELABORA

1. Una granja tiene gallinas y conejos, en total hay 35 animales y 116 patas. ¿Cuántas gallinas y conejos hay?
2. En un prado se quiere cercar una zona rectangular para que paste una cabra. Se tienen 24 m de valla y queremos que el área del recinto delimitado sea de 32 m2. Calcula las dimensiones de la zona vallada.

Cuando ya tengas soltura en la resolución de problemas de dos ecuaciones con dos incógnitas no es necesario que realices todos los pasos, con escribir las ecuaciones es suficiente. De esta forma puedes seguir resolviendo todos los problemas que se resuelvan mediante un sistema de dos ecuaciones con 2 incógnitas.

3. PROCEDIMIENTO DE RESOLUCIÓN DE PROBLEMAS MEDIANTE SISTEMAS 3×3

Sesión 1

EXPLICA

Hemos comprado un videojuego, unos auriculares y una mochila. El precio de los auriculares es

el doble del precio del videojuego, y también es el triple de la diferencia del precio de la mochila

y el videojuego. Considerando que hemos pagado 70 €, calcula los precios de los tres artículos.

Abre el applet: Procedimiento de resolución de problemas mediante sistemas 3×3

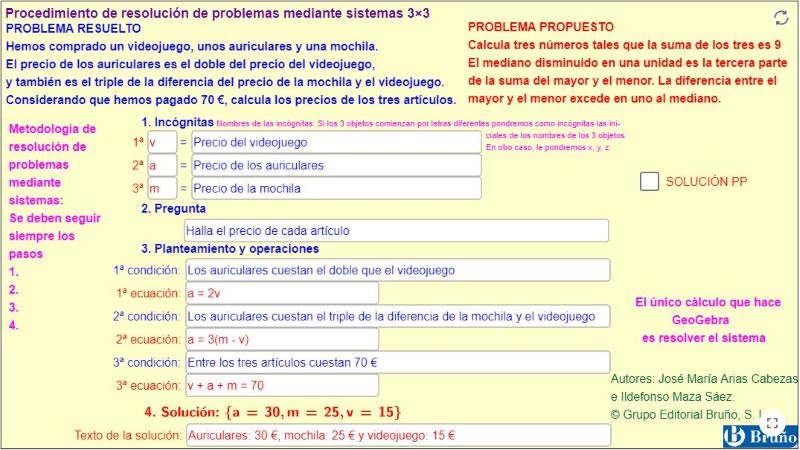
Analiza la resolución del PROBLEMA RESUELTO mediante la descomposición de las siguientes partes:

1. Incógnitas: se escriben los conceptos de las incógnitas.
2. Metodología y didáctica: Si los objetos comienzan por letras diferentes, pondremos como incógnitas las iniciales de sus nombres. En otros casos pondremos x, y, z, si conocemos qué valor es el menor, el mediano y el mayor, debemos asociar el valor de la 1.ª incógnita x al valor más pequeño, el de y al mediano y el de z al mayor. Estas recomendaciones ayudan a los alumnos a centrarse en el problema y adquieren mucha más soltura en la resolución de problemas algebraicos.
3. Pregunta: se escribe la pregunta o preguntas.
4. Planteamiento y operaciones: se escriben las relaciones o condiciones que se convierten en ecuaciones formando un sistema y se resuelve.
5. Solución: se escriben la solución con las unidades y se comprueba que son coherentes y que se cumplen las relaciones dadas.

ELABORA

Resuelve el PROBLEMA PROPUESTO y comprueba la solución.

Sesión Final

Al igual que en los problemas de ecuaciones y en los sistemas 2×2, resuelve los siguientes problemas escribiendo solo las ecuaciones.

ELABORA

1. Un hotel adquirió un total de 200 unidades entre almohadas, mantas y edredones, gastando un total de 7500 euros. El precio de una almohada es de 16 euros, el de una manta es de 50 euros y el de un edredón es de 80 euros. Además, el número de almohadas compradas es igual al número de mantas más el número de edredones. ¿Cuántas almohadas, mantas y edredones ha comprado el hotel?
2. El cajero automático de una determinada entidad bancaria solo admite los siguientes billetes de 50, 20 y 10 €. Los viernes depositan en el cajero 225 billetes por un importe total de 7000 €. Averigua el número de billetes de cada valor depositado, sabiendo que la suma del número de billetes de 50 y de 10 € es el doble del número de billetes de 20 € Cuando ya tengas soltura en la resolución de problemas de 3 ecuaciones con 3 incógnitas no es necesario que realices todos los pasos, con escribir las ecuaciones es suficiente. De esta forma puedes seguir resolviendo todos los problemas que se resuelvan mediante un sistema de 3 ecuaciones con 3 incógnitas.

JUSTIFICACIÓN DE ESTA SITUACIÓN DE APRENDIZAJE SOBRE LA RESOLUCIÓN DE PROBLEMAS ALGEBRAICOS

Esta situación de aprendizaje sobre la resolución de problemas algebraicos es una herramienta eficaz para integrar los elementos curriculares de la resolución de problemas mediante tareas y actividades significativas y relevantes para resolver problemas de manera creativa y cooperativa, reforzando la autoestima, la autonomía, la reflexión y la responsabilidad. Se parte primero de la resolución de problemas con una sola incógnita, luego de problemas utilizando 2 incógnitas o variables y por último tres variables y está convenientemente contextualizada y es muy respetuosa con el proceso de desarrollo integral del alumnado en todas sus dimensiones, teniendo en cuenta sus potencialidades, intereses y necesidades, así como las diferentes formas de comprender la realidad como se muestra en los enunciados de los problemas utilizados.

Esta situaciones de aprendizaje plantea un reto o problema de cierta complejidad en función de la edad y el desarrollo del alumnado, cuya resolución creativa implica la movilización de manera integrada de los saberes básicos (conocimientos, destrezas y actitudes), a partir de la realización de distintas tareas y actividades.

El planteamiento es claro y preciso en cuanto a los objetivos que se espera conseguir y los saberes básicos que hay que movilizar. El escenario de desarrollo está bien definido y facilita la interacción entre iguales, para que el alumnado pueda asumir responsabilidades individuales y trabajar en equipo en la resolución del reto planteado, desarrollando una actitud cooperativa y aprendiendo a resolver de manera adecuada los posibles conflictos que puedan surgir.

Esta situación de aprendizaje favorece la transferencia de los aprendizajes adquiridos a la resolución de un problema de la realidad cotidiana del alumnado, en función de su progreso madurativo.

En su diseño, se facilita el desarrollo progresivo de un enfoque crítico y reflexivo, así como el abordaje de aspectos relacionados con el interés común, la sostenibilidad, el respeto a la diferencia o la convivencia, se puede iniciar un diálogo y la búsqueda de consenso. De igual modo, se tienen en cuenta las condiciones personales, sociales o culturales del alumnado, para detectar y dar respuesta a los elementos que pudieran generar exclusión. El profesorado y el personal educador y formador debe proponer retos que hay que resolver, bien contextualizados y basados en experiencias significativas, en escenarios concretos y teniendo en cuenta que la interacción con los demás debe jugar un papel de primer orden. El alumnado enfrentándose a estos retos irán estableciendo relaciones entre sus aprendizajes, lo cual les permitirá desarrollar progresivamente sus habilidades lógicas y matemáticas de medida, relación, clasificación, ordenación y cuantificación; primero, ligadas a sus intereses particulares y, progresivamente, formando parte de situaciones de aprendizaje que atienden también a los intereses grupales y colectivos.

LOMLOE

Saberes básicos.

1. Sentido algebraico.

Pensamiento computacional.

• Formulación, resolución y análisis de problemas de la vida cotidiana y de la ciencia y la tecnología utilizando herramientas o programas adecuados.
• Comparación de algoritmos alternativos para el mismo problema mediante el razonamiento lógico

Arias Cabezas, J. M. y Maza Sánchez, I. (2023). Matemáticas I, 1º de Bachillerato de Ciencias y Tecnología, Nueva etapa. Madrid, Ed Bruño del Grupo ANAYA.

Arias Cabezas, J. M. y Maza Sánchez, I. (2023). Matemáticas Aplicadas a las Ciencias Sociales I, 1º de Bachillerato de Sociales, Nueva etapa. Madrid, Ed Bruño del Grupo ANAYA.

Arias Cabezas, J. M. y Maza Sánchez, I. (2023). Matemáticas II, 2º de Bachillerato de Ciencias y Tecnología, Nueva etapa. Madrid, Ed Bruño del Grupo ANAYA.

Arias Cabezas, J. M. y Maza Sánchez, I. (2023). Matemáticas Aplicadas a las Ciencias Sociales II, 2º de Bachillerato de Sociales, Nueva etapa. Madrid, Ed Bruño del Grupo ANAYA.

José María Arias Cabezas
Catedrático de Matemáticas de Instituto de Secundaria. Profesor del Máster de Formación del Profesorado de Secundaria de la Universidad Autónoma de Madrid. Asignatura: TICM: Tecnologías de la información y la comunicación aplicadas a la educación matemática de ESO y Bachillerato. Investigador del IUCE de la UAM en TIC aplicadas a ESO y Bachillerato en Matemáticas. Autor de Matemáticas de ESO y Bachillerato de la editorial Bruño del grupo ANAYA. Ha sido Director General de ESO y Bachillerato del MEC de España.

chemarias.com